Moment bezwładności a wózek do przerzutki SHURIKEN
Data dodania: 05-04-2019
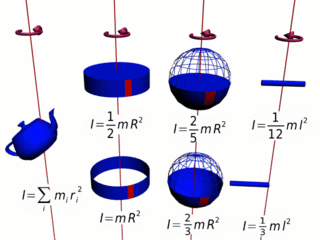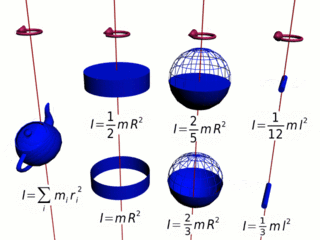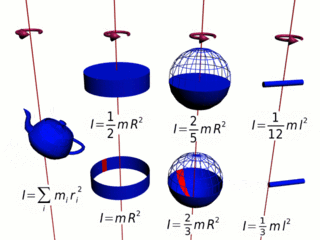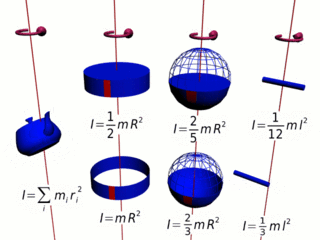


Moment bezwładności ciała składającego się z n cząstek jest równy sumie momentów bezwładności każdej z cząstek względem określonej osi obrotu:

Na przykład dla ciała składającego się z czterech cząstek, mamy:
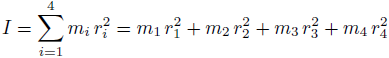
gdzie m1, m2, m3 i m4 to masy cząstek, z których składa się ciało, r1, r2, r3 i r4 to odległość od osi obrotu odpowiednio cząstki o masie m1, m2, m3 i m4.
A wiec zajmijmy się wyliczeniami w naszym SHURIKEN'ie
Aby było łatwiej zakładamy, że masa jednego elementu łańcucha wynosi 5 gram
1) Na początek, abyśmy mieli porównanie zróbmy obliczenia dla zwykłego standardowego małego kółeczka, które zazwyczaj są w naszych przerzutkach: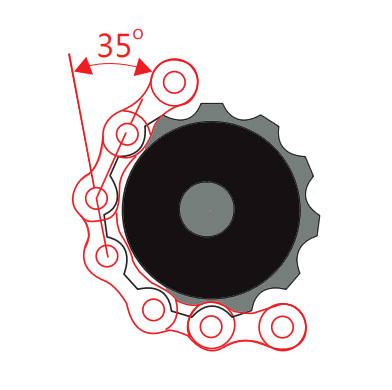
r = 2,1 cm
m = 10 gram (2 elementy łańcucha)
I = 44,1 g/cm2
2) Zajmijmy się teraz górnym kółeczkiem przerzutki. W SHURIKEN ma rozmiar 12T. Testy wykazały że jest to optymalna wielkość. Większe kółko w tym przypadku nie gwarantuje płynnej zmiany przełożeń.
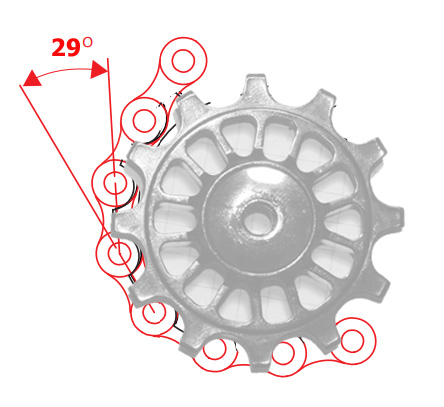
r = 2,6cm
m = 12,5 gram (2,5 elementy łańcucha)
I = 84,5 g/cm2

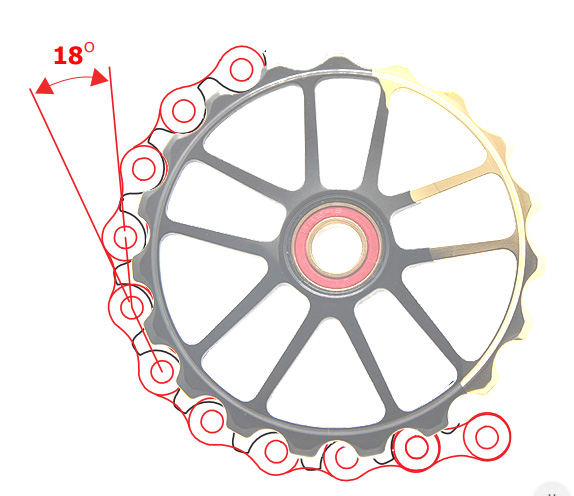
r = 3,8 cm
m = 22,5 gram (4,5 elementy łańcucha)
I = 324,9 g/cm2


Przejdź do strony głównej Wróć do kategorii 4) Przerzutki
Wózki do przerzutek z niestandardowymi kółeczkami nie bez powodu zdobywają uznanie wśród kolarzy, zwłaszcza szosowych. Prócz ich ponadprzeciętnego wyglądu odwdzięczają się wysoką kulturą pracy, bardzo niskimi oparami toczenia, ale i również dzięki małemu kątowi linii łańcucha oszczędnością energii. SHURIKEN TOKEN'a pod tym względem wiedzie prym wśród tego typu wózków dostępnych na rynku.
Jest jeszcze jeden znaczący czynnik przemawiający za wielkimi kółeczkami. Pozwala zaoszczędzić naszą energię podczas długiej i szybkiej jazdy, To MOMENT BEZWŁADNOŚCI MASY. Im jest większy tym na dłuższych dystansach pomaga (choć troszeczkę) zmniejszyć zmęczenie. Ma również wpływ w jeździe na czas oraz bez wątpienia w triatlonie.
Jest jeszcze jeden znaczący czynnik przemawiający za wielkimi kółeczkami. Pozwala zaoszczędzić naszą energię podczas długiej i szybkiej jazdy, To MOMENT BEZWŁADNOŚCI MASY. Im jest większy tym na dłuższych dystansach pomaga (choć troszeczkę) zmniejszyć zmęczenie. Ma również wpływ w jeździe na czas oraz bez wątpienia w triatlonie.

Moment bezwładności (I), to wielkość fizyczna charakterystyczna dla ruchu obrotowego. Wielkość ta przyjmuje stałą wartość dla danego ciała i określonej osi jego obrotu. Wartość momentu bezwładności zależy od masy ciała, położenia osi obrotu, wokół której obraca się ciało oraz od rozkładu (rozmieszczenia) jego masy. M. Im większa wartość momentu bezwładności, tym trudniej jest wprawić albo zmienić ruch obrotowy danego ciała. Ale już wprawione ciało w ruch (w dużym uproszczeniu) "napędza" nam cały układ powodując płynniejszą pracę.
W rowerze moment bezwładności ma znaczenie we wszystkich elementach, które się obracają. Z oczywistych względów największą rolę odgrywa w kołach roweru. Nie można jednak pominąć pracy kółeczek przerzutki. Obracają się one ze znacznie większą prędkością niż koła. Wbrew pozorom wiele od nich zależy.
Wzór na moment bezwładności wygląda tak:
W rowerze moment bezwładności ma znaczenie we wszystkich elementach, które się obracają. Z oczywistych względów największą rolę odgrywa w kołach roweru. Nie można jednak pominąć pracy kółeczek przerzutki. Obracają się one ze znacznie większą prędkością niż koła. Wbrew pozorom wiele od nich zależy.
Wzór na moment bezwładności wygląda tak:
gdzie: m -masa, r- odległość masy od osi obrotu
W przypadku wózka przerzutki SHURIKEN rozkład masy na kółeczkach z grubsza przedstawia się tak:
W przypadku wózka przerzutki SHURIKEN rozkład masy na kółeczkach z grubsza przedstawia się tak:

Moment bezwładności ciała składającego się z n cząstek jest równy sumie momentów bezwładności każdej z cząstek względem określonej osi obrotu:

Na przykład dla ciała składającego się z czterech cząstek, mamy:
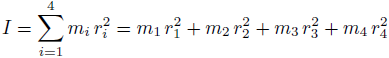
gdzie m1, m2, m3 i m4 to masy cząstek, z których składa się ciało, r1, r2, r3 i r4 to odległość od osi obrotu odpowiednio cząstki o masie m1, m2, m3 i m4.
A wiec zajmijmy się wyliczeniami w naszym SHURIKEN'ie
Aby było łatwiej zakładamy, że masa jednego elementu łańcucha wynosi 5 gram

1) Na początek, abyśmy mieli porównanie zróbmy obliczenia dla zwykłego standardowego małego kółeczka, które zazwyczaj są w naszych przerzutkach:

r = 2,1 cm
m = 10 gram (2 elementy łańcucha)
I = 44,1 g/cm2
2) Zajmijmy się teraz górnym kółeczkiem przerzutki. W SHURIKEN ma rozmiar 12T. Testy wykazały że jest to optymalna wielkość. Większe kółko w tym przypadku nie gwarantuje płynnej zmiany przełożeń.

r = 2,6cm
m = 12,5 gram (2,5 elementy łańcucha)
I = 84,5 g/cm2

3) Teraz możemy poszaleć ;-). Dolne kółeczko przerzutki SHURIKEN ma rozmiar. 19T. To kawał solidnego kółeczka, które toczy się na sprawdzonych łożyskach TBT. Jak w jego przypadku wyjdą obliczenia ?

r = 3,8 cm
m = 22,5 gram (4,5 elementy łańcucha)
I = 324,9 g/cm2

Podsumowując. Przyrost momentu bezwładności wraz ze wzrostem średnicy kółeczek jest znaczny. Możemy go wykorzystać na naszą korzyść. Na długich trasach, czasówkach oraz w triatlonie wózek do przerzutki SHURIKEN będzie Twoim motorem napędowym ;-)

*****
#wózek #do #przerzutki #shutiken #shimano #karbonowy #ceramicspeed #ceramic #speed #najlepszy
#wózek #do #przerzutki #shutiken #shimano #karbonowy #ceramicspeed #ceramic #speed #najlepszy
Komentarze (1)
Robkar95 02-02-2023 22:22:13
Bzdura. Im większe kółeczka to większy moment bezwładności. Więcej łańcucha jest w ruchu obrotowym. Ta energię która włożymy w ruch obrotowy koleczek nie odzyskamy. Stracimy tylko na przyspieszeniu.
Przejdź do strony głównej Wróć do kategorii 4) Przerzutki



 E-mail:
E-mail: Telefon
Telefon